Background
Autoregressive models generate sequences by predicting the next token in the sequence based on previous tokens. In each step of generation, the model processes the sequence up to the current token to predict the next one.
Problem Statement
The statement in question is:
“This autoregressive nature of the Decode stage contributes to longer processing times, and the computational expense scales quadratically with the total sequence length.”
Proof
- Notation and Assumptions:
- Let L be the total length of the sequence.
- Assume the model uses a mechanism where each token prediction requires processing the entire sequence up to that token.
- Computational Cost per Token:
- For each token i in the sequence (where i ranges from 1 to L), the model needs to process the sequence up to i. This implies that the cost of predicting the i-th token depends on i tokens.
- Thus, the cost for predicting the i-th token is proportional to i.
- Total Computational Cost:
- To find the total computational cost, sum the costs for each token prediction:

This is an arithmetic series sum, which can be simplified using the formula for the sum of the first L positive integers:

4. Scaling Behavior:
- The formula L(L+1)/2 simplifies to (L^2 + L)/2
- For large L, the L^2 term dominates, so the total cost scales quadratically with L:
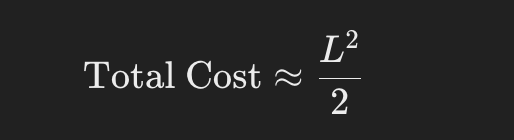
Conclusion
The computational expense of generating a sequence in an autoregressive model indeed scales quadratically with the sequence length ( L ), confirming the statement that processing times and computational expenses increase quadratically with the total sequence length.